Skip List

跳表是在链表的基础上做了改进，以提升查询的效率。跳表必须是有序的（这里假定是升序）。

跳表采用了 hierarchy 的结构，每一层都是一个链表。每个节点一定都会出现在最底层，提升到上一层的概率是常数 $p$ 。这样随着层数的增加，该层的节点个数会逐渐减少。

记在 $n$ 个节点的跳表中，期望包含 $\frac{1}{p}$ 个元素的层为第 $L(n)$ 层，则 $L(n) = \log_\frac{1}{p} n$ （此即跳表的期望层数）。

查找查询时从跳表的最高层开始，比较当前节点与目标节点。如果恰好等于，那么就找到了目标节点；如果小于，那么继续在该层中比较下一个节点；如果大于，就跳到下一层中进行比较。如果直到底层都还没找到，就说明目标节点不存在。可见，相对于链表，跳表在查询过程中接近目标的速度更快。期望时间复杂度为 $O(\log n)$ ，最差时间复杂度为 $O(n)$ 。

插入 / 删除 和查找的方式类似，都是先找到目标节点，然后在该位置进行修改、插入或者删除。

参考文章¹

Set

A set is an unordered collection of distinct values.

上面这句是老师 PPT 里给的数学上的集合定义，之前刷 LeetCode 的时候知道了，std 里的 set 原理是这样的。

Bloom Filter

布隆过滤器是基于哈希表的原理，查询效率是常数级的。

用一个长度为 $m$ 个比特位的数组来做标记， $k$ 个哈希函数来做映射。插入时，把插入的元素用这 $k$ 个哈希函数生成对应的哈希值，对 $m$ 取模后把数组中对应位置都标记成 $1$ ；查询时，只需对这个查询值同样做一次，看看数组中对应的几个位置是不是都是 $1$ 即可。

显见，布隆过滤器说没有的，一定没有；说有的，可能没有。 且布隆过滤器不支持删除。

设计布隆过滤器时，最优的哈希函数个数期望为 $k = \frac{m}{n} \ln 2$ ，其中 $n$ 是插入的元素个数。

在我们这学期的 LSM-tree 里，SSTablehead 就放了布隆过滤器（虽然是实现好的）。

AVL Tree

BST 的升级版，使树保持平衡。

平衡因子 = 左子树高度 - 右子树高度，若平衡因子的绝对值大于 $1$ ，说明树失衡。解决失衡问题需要对树进行左旋和右旋两种操作，图中左旋旋转的是节点5，右旋旋转的是节点14。

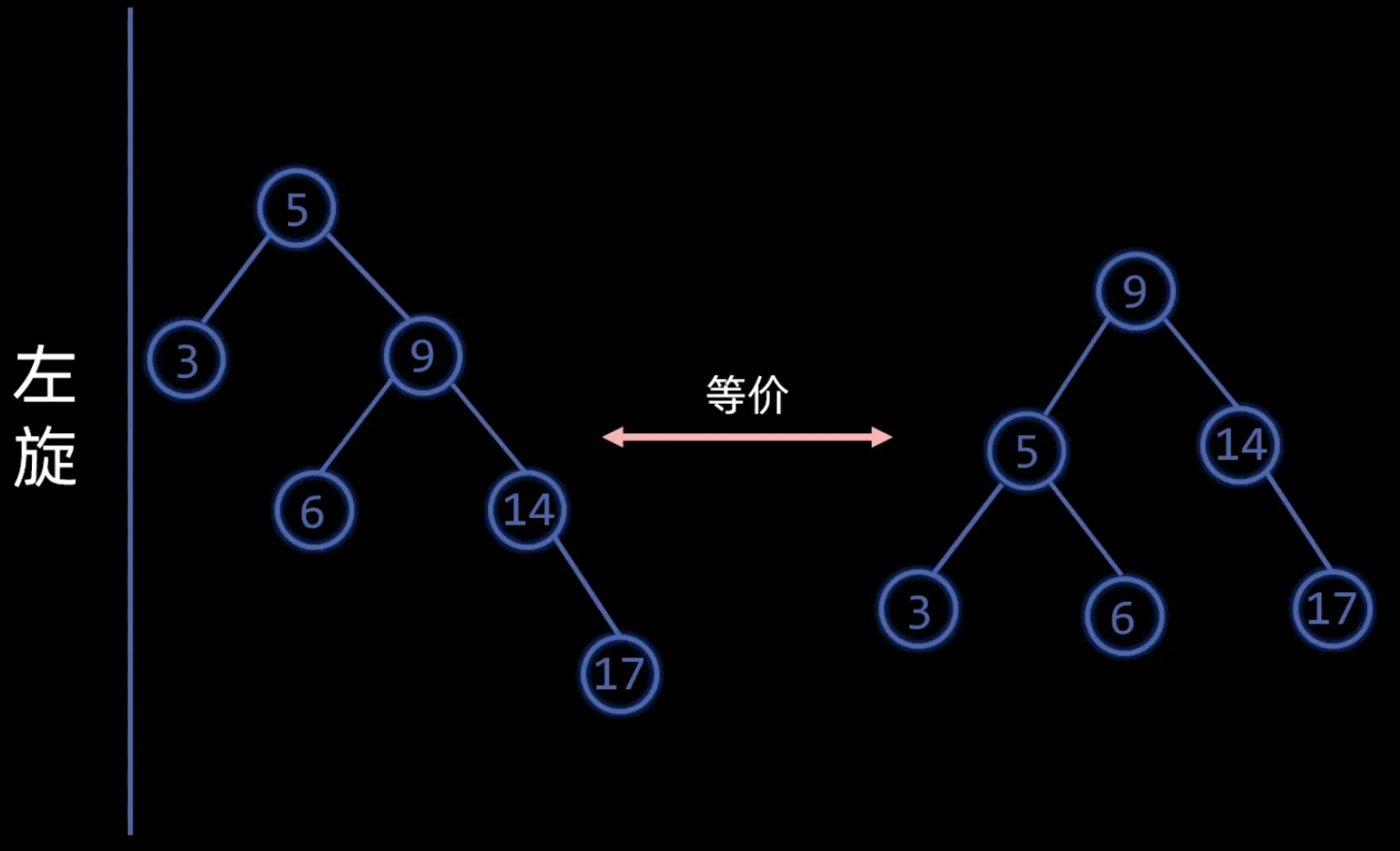
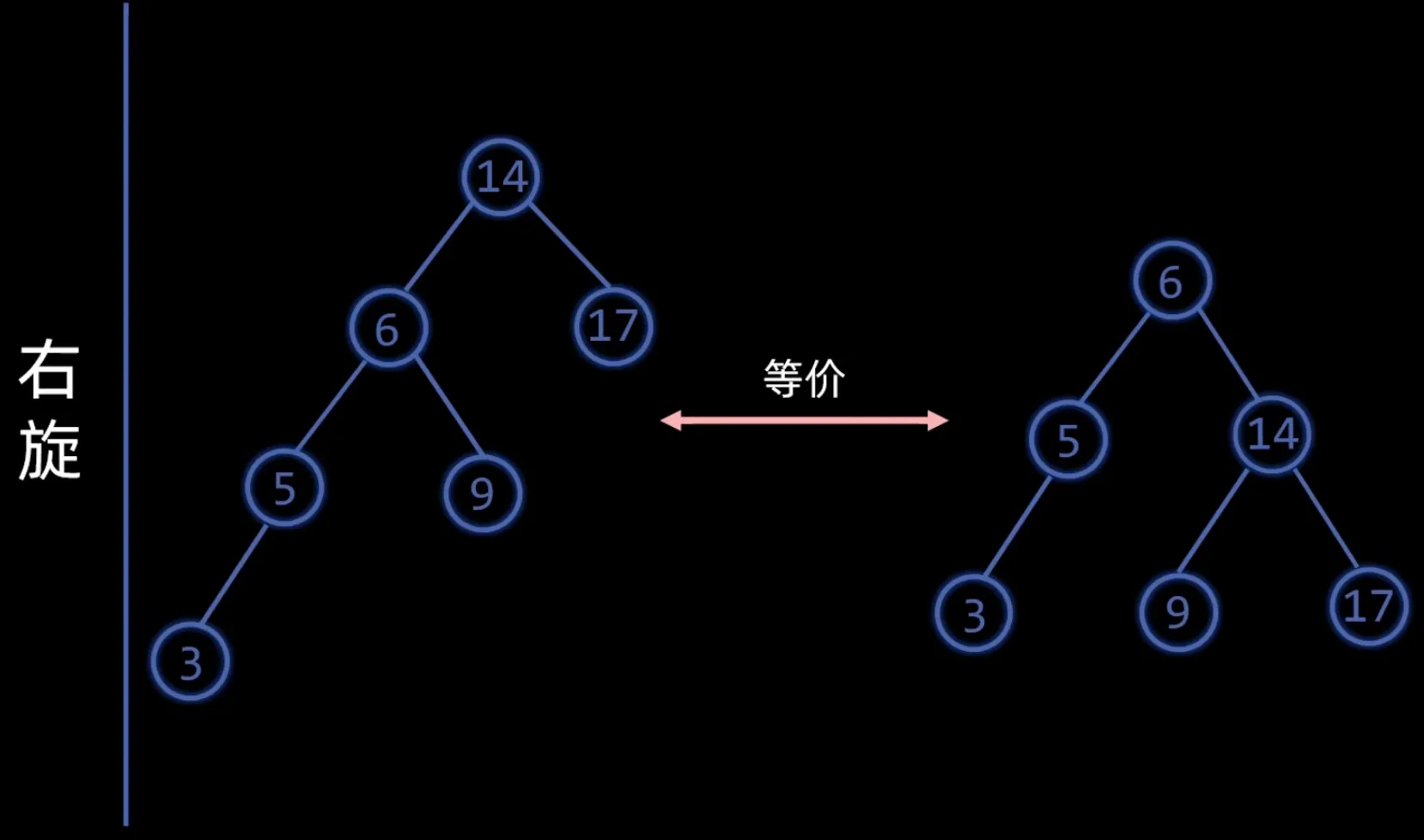
失衡有四种情况：

LL型 失衡节点平衡因子 = 2 && 失衡节点左孩子平衡因子 = 1，需要对失衡节点进行一次右旋；
RR型 失衡节点平衡因子 = -2 && 失衡节点左孩子平衡因子 = -1，需要对失衡节点进行一次左旋；
LR型 失衡节点平衡因子 = 2 && 失衡节点左孩子平衡因子 = -1，需要对失衡节点的左孩子进行一次左旋，然后对失衡节点进行一次右旋；
RL型 失衡节点平衡因子 = -2 && 失衡节点左孩子平衡因子 = 1，需要对失衡节点的右孩子进行一次右旋，然后对失衡节点进行一次左旋。

插入时若发生失衡，只需调整距离插入节点最近的失衡节点；删除时则需依次对每个祖先检查并调整。

这其实是我们大一就学过的数据结构，但是我有点忘了，顺带复习一下。

参考视频²

Splay Tree

伸展树的想法是，最近被访问到的节数据很可能很快被再次访问，因此每次查询后都要把被查询的节点旋转到根节点。

旋转操作和 AVL 树类似，有三种 splay 操作：

zig 被访问节点是根节点的孩子时进行，只需一次旋转即可将被访问节点移到根节点；
zig-zig 有点类似于 AVL 树中的 LL 和 RR 情形，需要依次对祖父和父亲进行一次旋转；
zig-zag 类似于 LR 和 RL。

为使被查节点成为根节点，每次查询后可能需要进行多次的伸展操作。

相比于 AVL 树，伸展树并不是严格平衡的。

Red-Black Tree

红黑树要满足五个性质：

所有节点必为红或黑；
根节点为黑；
叶子结点（NULL）为黑；
红色节点的子节点必为黑（不能有两个连续的红色节点）；
任意节点到 NULL 节点的每条路径上的黑色节点数量相同。

性质5保证了任意节点左右子树的高度差不超过两倍（最长路径不超过最短路径的两倍）。

新插入的节点默认为红色，只有可能破坏性质2或4，有三种情况：

插入的是根节点，直接变黑即可；
插入节点的叔叔是红色，此时需要把叔父爷都变色，然后把爷爷当做插入节点递归向上判断并维护；
插入节点的叔叔是黑色，此时需要根据 LL、RR、LR、RL 四种形态进行判断，做出对应的旋转操作，然后把最后一次旋转的旋转点和旋转中心点进行变色。

参考视频³

K-D Tree

K-D Tree 的每个节点都有 $k$ 个维度，可以用于对 $k$ 维空间的划分，最常见的是 $k = 2$ 。

假设我们已经知道了 $k$ 维空间内的 $n$ 个不同的点的坐标，要将其构建成一棵 K-D Tree，步骤如下：

若当前超长方体中只有一个点，返回这个点。
选择一个维度，将当前超长方体按照这个维度分成两个超长方体。
选择切割点：在选择的维度上选择一个点，这一维度上的值小于这个点的归入一个超长方体（左子树），其余的归入另一个超长方体（右子树）。
将选择的点作为这棵子树的根节点，递归对分出的两个超长方体构建左右子树，维护子树的信息。

通常 K-D Tree 的构建有两个优化策略：

轮流选择 $k$ 个维度，以保证在任意连续 $k$ 层里每个维度都被切割到。
每次在维度上选择切割点时选择该维度上的中位数，这样可以保证每次分成的左右子树大小尽量相等。

参考文章⁴

中位数算法

众数

这里众数的定义为在一组数中出现次数超过一半的数。在高效的中位数算法未知之前，确定众数候选采用 多数投票算法。

若在向量 A 的前缀 P（ |P| 为偶数）中，元素 x 出现的次数恰占半数，则 A 有众数，仅当对应的后缀 A − P 有众数 m，且 m 就是 A 的众数。

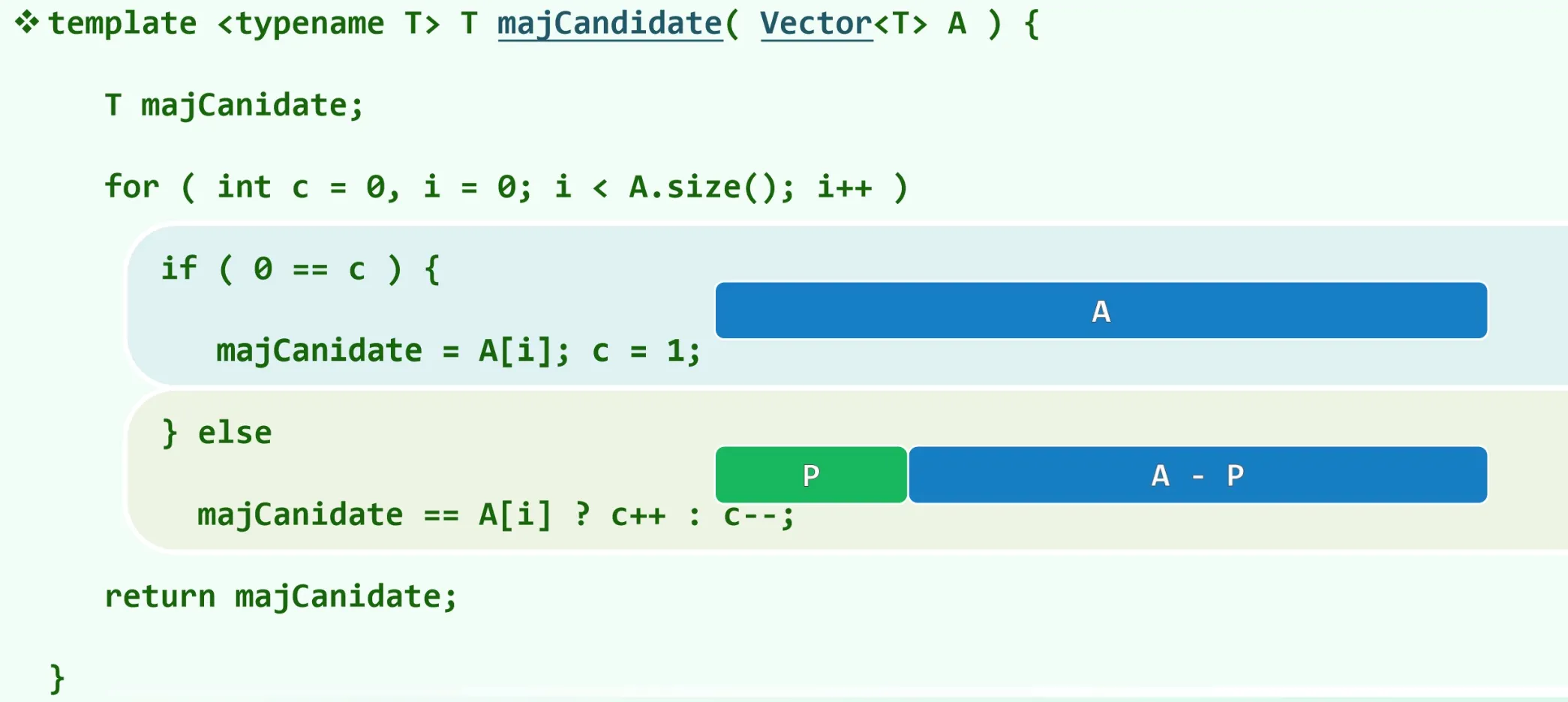
选出候选者后，还要再验证一次充分性，确定是否是真的众数。

事实上，众数一定是中位数，所以也可以通过高效的中位数算法来确定候选众数。

中位数

在长度为 $n$ 的向量 $S$ 中，元素 $S(\left \lfloor \frac{n}{2} \right \rfloor )$ 即为其中位数。

中位数是 k 选择算法中最复杂的一种情况。可以用堆排序来找到中位数，但效率太低。

Quick Select

快速选择的思想类似于快排，每次都选一个 pivot，把它移到它所处的百分位上，若所处位置恰好是 $k$ ，则找到。否则，只需要对其中一侧递归执行上述操作。

好的情况下时间复杂度为 $O(n)$ ，但最差情况（已排好序的数组）下会退化到 $O(n^2)$ 。

Linear Select

基于 BFPRT 算法（又叫 Median of Medians）的中位数选取算法，主要思想是把向量按每 $Q$ 个分成 $\left \lceil \frac{n}{Q} \right \rceil$ 组，然后每组都排序后取得中位数，把这些取出来的数作为新向量重复上述操作，直到得到最终的中位数。

这个算法的时间复杂度是 $O(n)$ 的，在最坏情况下性能优于快速选择，但在乱序数据上快速选择的性能普遍更优。

Topological Sort

DFS

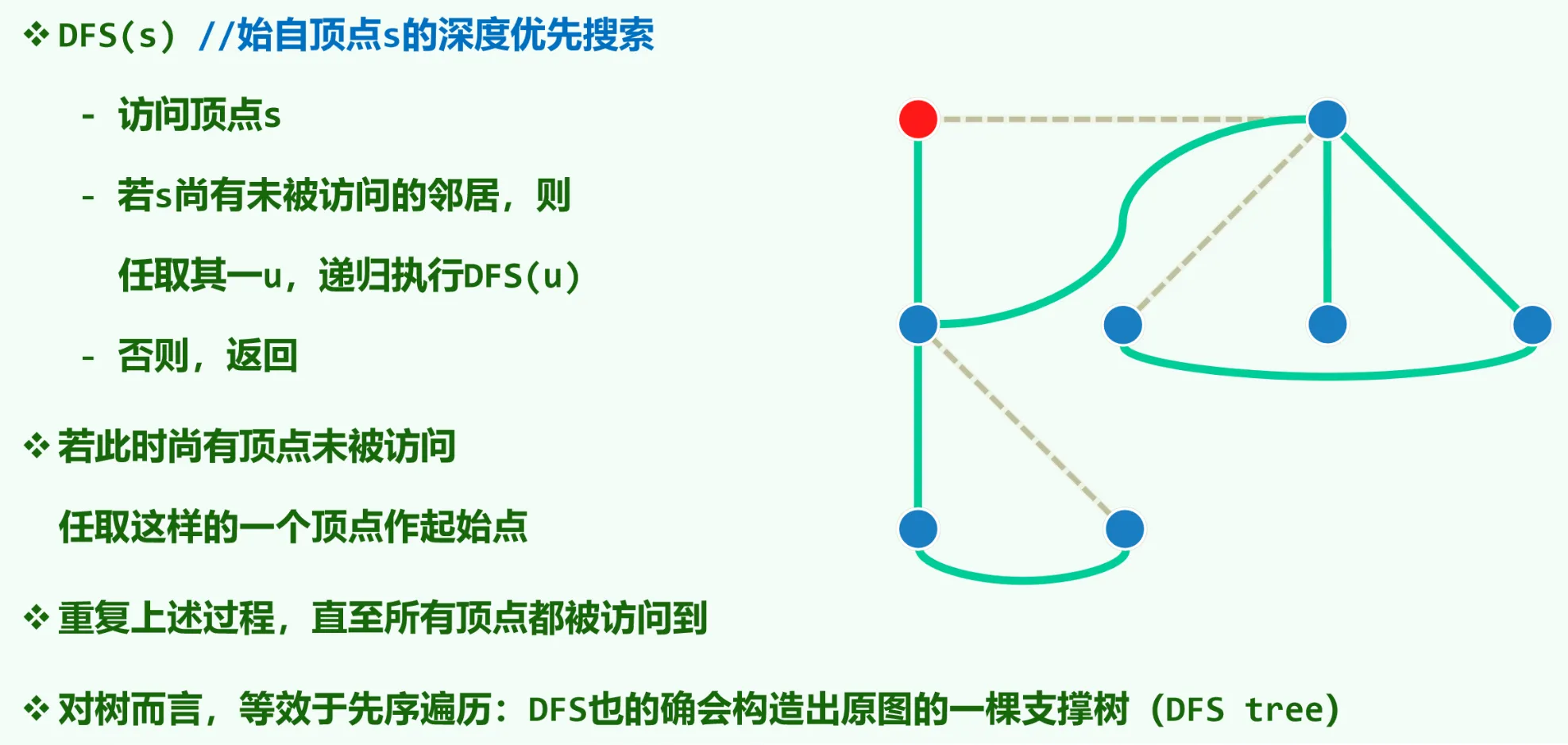
拓扑排序解决的是如何给一个有向无环图（DAG）的所有节点排序，一个经典的应用是找到一门课的所有先修课。

拓扑排序可以通过零入度算法实现，具体做法是，每次都选择一个入度为0的点（如果有多个，任选其一即可），然后删除这个点和它的出边。

拓扑排序可以用于判断一个图是否有环，一旦图中还有剩余节点，但没有入度为0的点，说明图中有环。

拓扑排序也可以用零出度算法实现，原理从名字就能看出，过程和零入度算法类似。

参考视频⁵

Dijkstra’s Algorithm

Dijkstra 算法用于求解非负权图上单源最短路径。

求点 P 到其它点的最短路径，需要每次选距离 P 最近的点，然后更新。

参考文章⁶

参考视频⁷

KMP Algorithm

KMP 算法用于判断模式串 P 是否在文本串 T 中出现过。

具体做法见这里。

KMP 算法的时间复杂度是线性的。

参考视频⁸

Parallel Programming

#include <thread>

数据竞争 对共享变量（全局变量、静态变量、共享指针）进行了非原子性的操作时会产生数据竞争。当一个线程还没有完成对数据的操作，而另一个线程拿到旧值进行了重复操作，就会导致结果不符。

#include <mutex>

互斥锁 用于解决数据竞争，对可能发生竞争的地方，加上互斥锁，确保该数据不会被重复操作。

std::lock_guard<mutex> lck(mtx)在构造器中，传入一个互斥锁的引用，自构造完成之后，互斥锁便上了锁，直到lock_guard类生命周期结束（退出作用域）调用析构器时，传入的互斥锁便解锁。

有时候多线程加锁反而会造成程序性能下降，例如一个简单的多线程求和，频繁的加锁十分耗时，随着线程数的上升，还可能加剧锁和锁之间的冲突，造成性能极度下降。

#include <atomic>

原子操作 std::atomic<T>确保对类型T的操作是原子的，无需显式锁。

Cuckoo Hash

布谷鸟哈希是对普通哈希表中值冲突的一种优化方案。

布谷鸟哈希有一个哈希表和两个哈希函数 $h_1$ 和 $h_2$ ，且对任意插入的键 $k$ ，都保证 $h_1(k) \ne h_2(k)$ 。

插入当新键插入时，检查 $h_1(k)$ 和 $h_2(k)$ 里是否有至少一个空位，若有，则插入一个空位；否则，就将其中一个位置中原有的键踢出，使被踢出的键尝试插入到它的另一个空位里，若仍被占据，则重复上述操作，直到某个键可以正常地插入。当哈希表中过满时，插入有可能会遇到死循环，可以通过设置一个循环次数阈值的方式，一旦循环次数超过该阈值，就进行 rehash。

查找由插入的实现可知，只需检查待查键 $k$ 的 $h_1(k)$ 和 $h_2(k)$ 两个位置即可。

实际应用中可能会进行并行的查找，但如果在某个键被踢出却还没放入时发生了查找，那有可能得到不存在该键的结果，一种解决方法是 基于回溯的插入。假设插入键 A 时产生的踢出序列为 A->B->C->D->NIL，可以先踢出 D，依次向上直到 A，这样可以保证每个键一被踢出就能有空位插入，只要将某个键插入到指定位置的操作是原子的，就可以确保这些元素始终在哈希表里。

Parallel MST

最小生成树是边权和最小的生成树。

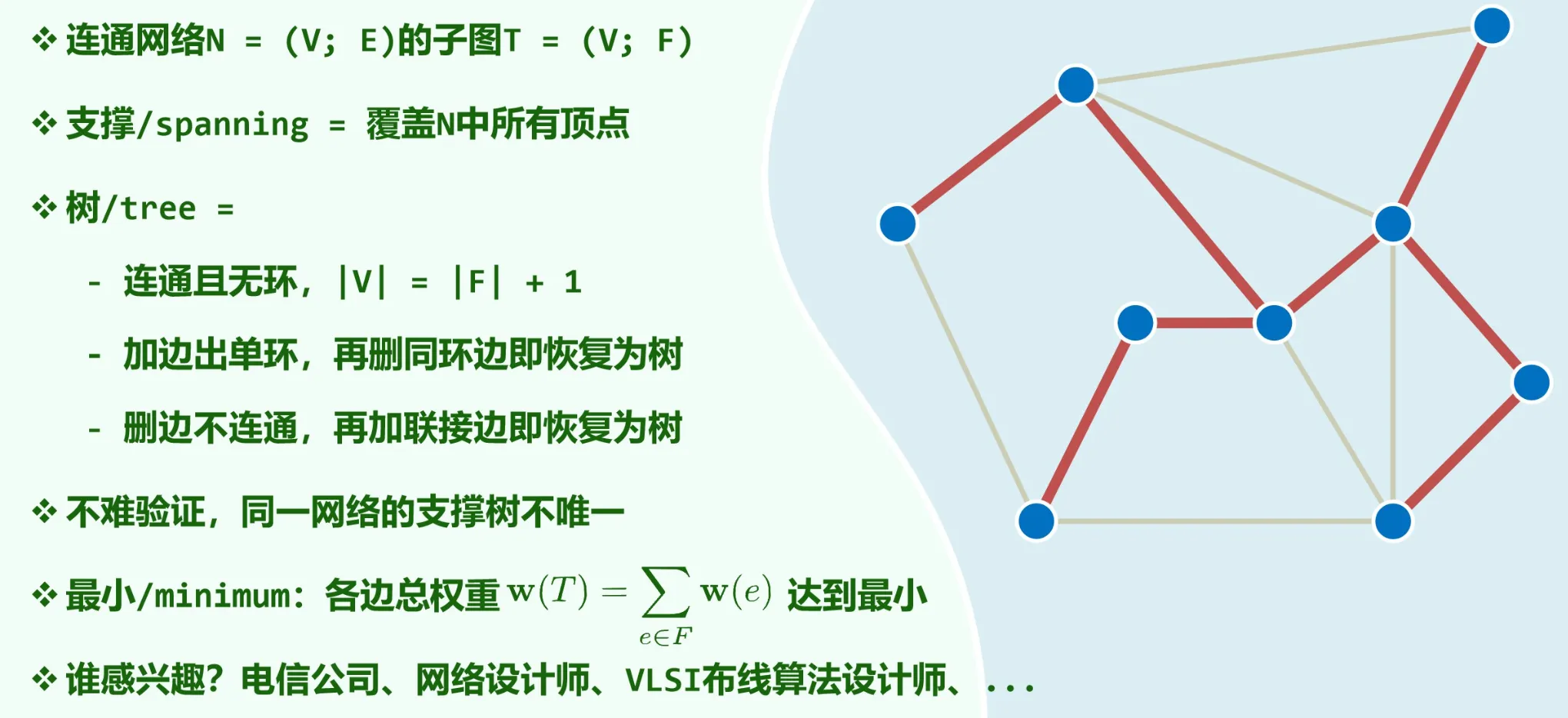
Prim’s Algorithm

Prim 算法的思想是，从一个节点开始，不断加点。步骤如下：

建立两个顶点集合 $X$ 和 $Y$ ，其中 $X$ 包含图中任意一顶点， $Y$ 包含其余所有顶点；
找出具有最小权重的边 $(x,y)$ ，其中 $x \in X, y \in Y$ ，然后把顶点 $y$ 从 $Y$ 移动到 $X$ ，并把边 $(x,y)$ 加入到最小生成树中；
重复上一步直到 $Y$ 为空，即得该图的最小生成树。

这个算法的时间复杂度为 $O(n^2)$ 。

并查集

把一组数分成多个互不相交的等价类，各由其中一个元素作为代表。

顾名思义，并查集支持两种操作：

合并（Union） 合并两个元素所属的类（合并对应的树）；
查询（Find） 查询某个元素所属的类（查询对应的树的根节点），可以用于判断两个元素是否属于同一集合。

Kruskal’s Algorithm

Kruskal 算法的思想是，从权重最小的边开始，从小到大依次加入到最小生成树中，如果某次加边会产生环，则舍弃该边，直到加入 $n - 1$ 条边，就得到了最小生成树。

判断加边后是否会产生环，需要用到并查集，把相互连接的点作为一个等价类，若尝试加入的边的两个端点本就属于同一个类，则说明会产生环，不允许加入。

这个算法的时间复杂度为 $O(m \log m)$ 。

条件变量

基于边的并行最小生成树算法

也可称作并行 Kruskal 算法，分为由各并行进程完成的“部分算法”和由一个全局进程完成的“仲裁算法”。

部分算法 各进程收到来自全局进程的消息后选出本分区当中具有最小权重的边并发送给全局进程，直到本分区没有待处理的边或收到全局进程的结束通知时结束进程；
仲裁算法
1. 全局进程首先向所有并行进程发送消息获取各分区最小权重边构成队列 Q；
2. 循环取出 Q 中权值最小的边 e，并向提供边 e 的进程发送消息请求补充新的最小权重边至 Q 中；
3. 如果取出的边 e加入到结果集 T 中不会构成环路则保留此边，若会构成环路则将其丢弃；
4. 当 T 中的边的数量为 $n - 1$ 或队列 Q 为空时算法结束，同时通知各进程结束算法。

Borůvka’s Algorithm

Borůvka 算法可以看做 Prim 算法和 Kruskal 算法的综合，步骤如下：

把所有点看成一个独立的连通分量；
对于每个连通分量，都找出权重最小的边（这个边一定是一端属于这个连通分量而另一端不属于的），把这条边加入到结果集中；
重复上一步直到整个图只剩一个连通分量。

这个算法的时间复杂度为 $O(m \log n)$ 。

基于顶点的并行最小生成树算法

分为由各并行进程完成的“分区 Prim 算法”以及由一个全局进程完成的“全局 Borůvka 算法”。

PageRank

PageRank 是早期 Google 搜索引擎的基础之一，其核心思想是：

一个网页的重要性取决于链接到它的其他网页的数量和质量。质量高的网页投出的“票”（链接）权重更高

该算法基于公式

PR(u) = \sum_{v \in D(u)} \frac{PR(v)}{|S(v)|},

其中， $PR(u),PR(v)$ 分别表示网页 $u,v$ 的 rank 值， $D(u)$ 表示指向 $u$ 的所有网页，也就是网页图中 $u$ 的入边源点集合， $S(v)$ 表示从 $v$ 出发指向的网页集合， $|S(v)|$ 就是该集合的大小。

实际应用中会引入一个阻尼系数 $d$ ，表示用户到达某个页面时继续浏览的概率，则 $1 - d$ 就是用户停在这个页面的概率，故公式可更新为

PR(u) = 1 - d + d \sum_{v \in D(u)} \frac{PR(v)}{|S(v)|}.

基于此公式对每个页面的 rank 值进行迭代，在各个顶点的 rank 值收敛时停止（设定迭代次数的阈值）。也可以用并行的方式，分配多个线程，每个线程负责计算指定顶点的 rank 值。

Search

ADS 期末复习